The purpose of this assignment is to learn to
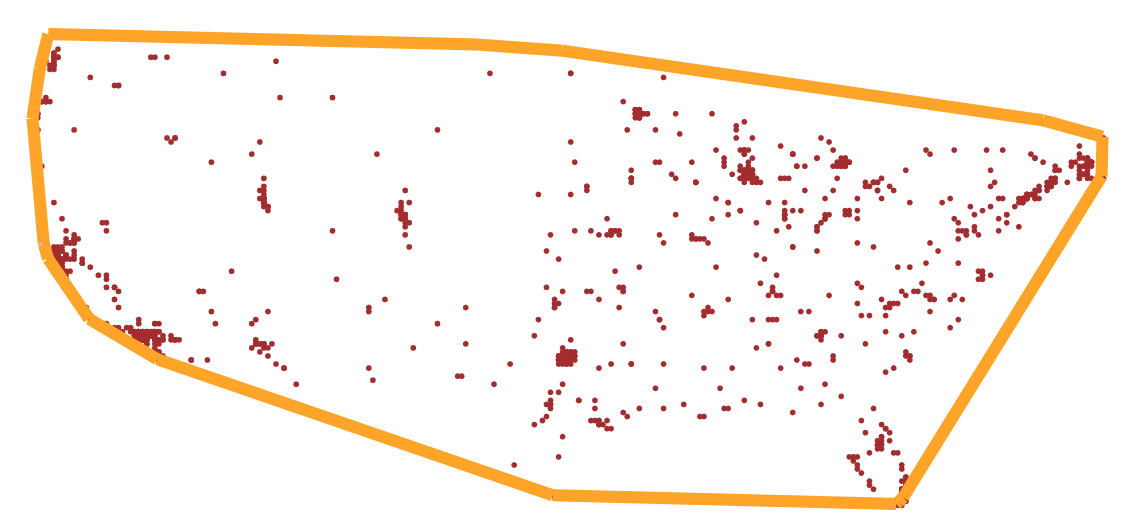
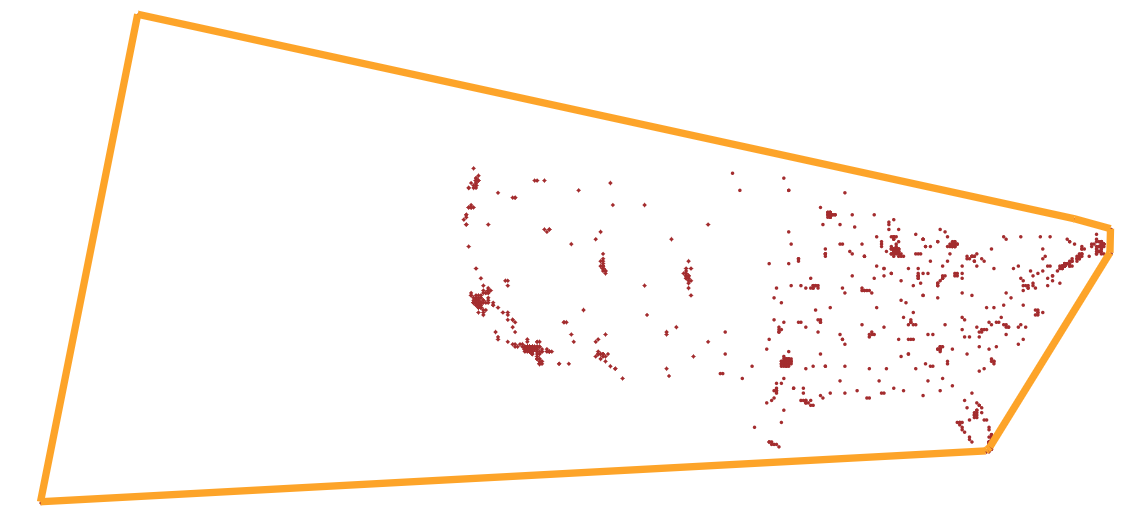
The convex hull The convex hull of a set of points can be defined as the tightest fitting polygon that encloses them. The goal is to identify the points and edges that make up this polygon. Here we will use the US city locations as 2D points to determine the convex hull. See the figures below that you will end up in the visualization:


This is the simpler but less efficient algorithm (O(N^2) and not appropriate for very large datasets. Its implementation is much simpler compared to the divide and conquer version (see below). The algorithm consists of iterating through each point and testing all line segments emanating from it as potential candidates. An edge is part of the convex hull, if all of the remaining points are to its 'left' (one sided). At the end of the process, you have the set of edges that make up the convex hull and are drawn to illustrate it.
We can use the line equation of the candidate edge and evaluate the point using the equation and look at its sign, which indicates the side of the line that point lies. If all points evaluate to the same side, we accept this edge as part of the convex hull.
The equation of a line (in 2D) is of the form
Ax + By + C = 0
where the point (x, y) is on the line. Any point that is not on the line is one side or the other and evaluating the above equation with such points will result in a value (actually a distance to the line) that is positive or negative. The coefficients, A, B and C are constants representing the direction cosines of the line (or the normal vector).
If pt1 and pt2 are two points that make up an edge, then then we can calculate the direction cosines as
A = pt2.y - pt1.y B = pt1.x - pt2.x C = pt1.xpt2.y - pt1.ypt2.x
A, B come from the slope (dy/dx), and C (intercept) is obtained by plugging
one of the line end points into the equation (the derivation is easier if
you start with y = mx + c, where m is the slope and c is the intercept.
The above form is more convenient for implementation.
Thus, the algorithm iterates with each point and forming edges with the rest of the points and checking the sign of the distance (result of evaluating the line equation) with the second end point of the potential edge). If all distances are of the same sign, then you accept that edge as part of the convex hull.
A more efficient algorthm to compute the convex hull is to use a divide and conquer strategy, which has been shown to achieve linear time (O(N)) in practice. It involves recursively subdividing the pointset into two subsets and exploiting geometric relationships to ignore large sets of points from consideration in the search for the edges that make up the convex hull
ToDo (Reference, Levitin, The Design and Analysis of Algorithms)
See the figures above for what the output will look like (with and without cities in Alaska and Hawaii):
SymbolCollection documentation
SymbolCollection documentation